嶨婰嶨妛屸妝幒 <<
傾儗僯僂僗偺朄懃偲恖娫偺庻柦
側傫偲両懱壏偲庻柦偵偼娭學偑偁傞偺偱偡丅
偪傚偭偲棟岺宯側僱僞偱偡丅
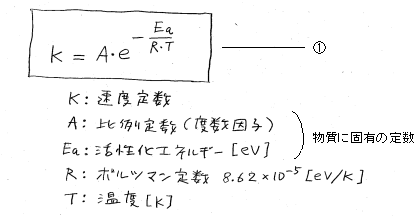
嘆幃偼傾儗僯僂僗偺幃偲尵傢傟偰偄傞幃偱偡丅偁傞愨懳壏搙T偵偍偗傞壔妛斀墳偺懍偝傪昞偟偰偄傑偡丅娙扨偵尵偆偲丄懡偔偺壔妛斀墳偼丄壏搙偑忋偑傞偲巜悢娭悢揑偵丄偦偺懍搙偼懍偔側傞傛丅偲尵偆偙偲傪昞尰偟偰偄傞偺偱偡丅傑偨丄偙偺幃偼丄扨弮側壔妛斀墳偩偗偱偼側偔丄怓乆側暔偑楎壔偡傞懍偝偵傕摉偰偼傑傞傜偟偄偱偡丅偙傟傪梡偄偰丄怓乆側暔乮岺嬈惢昳摍乯偺懴媣帋尡偵偍偄偰丄壏搙傪忋偘傞偙偲偵傛傝帋尡帪娫傪抁弅偝偣傞崻嫆偲偟偰梡偄傜傟偰偄傑偡丅
嘆幃偼懍搙掕悢傪昞偟傑偡偑丄偦偺媡悢乮楎壔懍搙偺媡悢乯傪偲傞偲丄偦傟偼丄偦偺暔懱偺庻柦乮怣棅惈傪堐帩偱偒傞帪娫乯傪昞尰偟偰偄傞偲尵偊傑偡丅壓偺嘇幃偺傛偆偵側傝傑偡丅乮媡悢偵偡傞偺偩偐傜丄巜悢晹偺晞崋傪斀懳偵偡傟偽傛偄傢偗偱偡丅乯
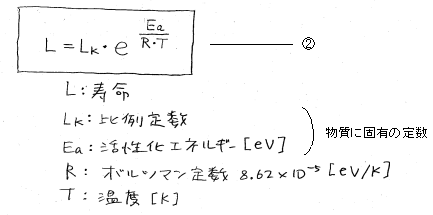
偙偙偱丄彮偟層嶶廘偄庻柦掕悢俴k傪徚嫀偡傞偨傔偵丄壏搙偺堎側傞2偮偺暔懱乮壏搙Tm偲壏搙Tn偺暔懱乯偺庻柦偺斾偱峫偊傞偙偲偵偟傑偡丅壏搙Tm偱偁傞暔懱俵偺庻柦Lm偲
丄壏搙Tn偱偁傞暔懱俶偺庻柦Ln偲偺斾偼壓偺嘊幃偺傛偆偵側傝傑偡丅
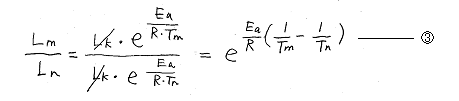
偲偙傠偱丄杔偨偪丄恖娫偺惗柦妶摦傕丄柍悢偺壔妛斀墳偺寢廤偲峫偊傞偙偲偑偱偒傑偡丅偱丄傆偲丄懱壏偺堘偄偵傛傝庻柦偑偳傟偩偗曄傢偭偰偔傞偺偐傪傾儗僯僂僗偺幃偱悇掕偱偒側偄傕偺偐丠偲巚偄偮偒傑偟偨丅偦偙偱丄嘊幃傪梡偄偰寁嶼偟偰傒傑偡丅
偙偺偲偒栤戣偵側傞偺偼丄惗暔乮恖娫乯偺惗柦妶摦偱偺妶惈壔僄僱儖僊乕偼偳傟偔傜偄偺抣偵偡傟偽偄偄偺偐丠偲偄偆媈栤偱偡丅僱僢僩偱専嶕偡傟偳傕丄柧妋側抣偼傒偮偐傝傑偣傫偱偟偨丅偦傕偦傕丄傾儗僯僂僗偺幃偵偍偗傞妶惈壔僄僱儖僊乕偲偄偆傕偺帺懱偑傗傗晄柧妋側懚嵼偺傛偆偱偡丅偱傕丄偲偁傞怣棅惈帋尡娭楢偺暥專偵乽晠怘丄晠攕楎壔偵偍偗傞妶惈壔僄僱儖僊乕偼0.3乣0.4eV偲偁傝傑偟偨丅偙傟偼丄側傫偲側偔惗暔妶摦偵嬤偄暤埻婥側偺偱丄偲傝偁偊偢丄偙偺抣偱寁嶼偟偰傒傞偙偲偵偟傑偡丅
椺偊偽丄懱壏35.5亷偺M偝傫偲丄懱壏37亷偺N偝傫偲偺庻柦傪斾妑偟偰傒傑偡丅
Tm=35.5+273=308.5K丄Tn=37+273=310K丄Ea=0.4eV丄R=8.62*10丱(-5)eV/K傪嘊幃偵戙擖偡傞偲
Lm/Ln=1.075丂偲側傝傑偡丅
偮傑傝丄懱壏35.5亷偺M偝傫偼丄懱壏37亷偺N偝傫
傛傝傕栺俉亾挿惗偒偱偒傞偲偄偆偙偲丅懱壏37亷偺N偝傫偑80嵨傑偱惗偒偨側傜丄懱壏35.5亷偺M偝傫偼86嵨傑偱惗偒傞偙偲偑偱偒傑偡丅偮傑傝1.5亷懱壏偑掅偄偲丄6擭庻柦偑挿偔側傞偲偄偆寢壥偵側傝傑偡丅懱壏偺掅偄恖偼丄彮偟挿惗偒偱偒偦偆偱偡丅
仭曗懌偱偡丅
偙傟偼丄恖娫傪偨傫側傞壔妛曄壔偺廤崌懱偲偟偰梀傃揑偵峫嶡偟偨傕偺偱偡丅
惗暔妛揑側峫嶡傗偦偺懠妛弍揑崻嫆偼堦愗偁傝傑偣傫丅
寬峃宯偺杮偵傛傞偲丄媡偵丄懱壏偑崅偄曽偑丄寣峴傪椙偔偟丄柶塽椡傪崅傔丄寬峃偵椙偄乮偮傑傝挿惗偒偱偒傞乯傜偟偄偱偡丅
偨傇傫丄暔棟壔妛揑側梫場傛傝傕丄惗暔妛揑側梫場丄偝傜偵偼怱棟妛揑乮惛恄妛揑乯梫場偺曽偑梱偐偵丄埑搢揑偵丄恖娫偺庻柦偵塭嬁傪梌偊偰偄傞偺偩偲巚偄傑偡丅
